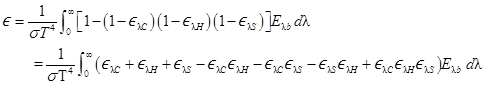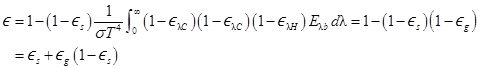UNIFORM SOOT SUSPENSION IN AN ISOTHERMAL RADIATING GAS

Usually, for soot in a flame or in combustion products, there are gaseous constituents that also radiate energy. To simplify the present discussion, it is assumed that only three radiating constituents are present—carbon dioxide, water vapor, and soot—but the method can be extended to more constituents. As spectral radiation passes through the gas-soot suspension, the local attenuation depends on the sum of the absorption coefficients so, from (9-65), the spectral emittance is

 

                                            (D-25)

 

where the subscripts C, H, and S refer to CO2, H2O, and soot. Then, from (D-12), the total emittance is

 

                                  (D-26)

 

With  for J = C, H, and S, this can be written in the equivalent forms

 

       (D-27)

 

The first three terms in the last integral yield the total emittances of the three constituents, so that

 

           (D-28)

 

A term such as λC λH is nonzero only in spectral regions where both kλC and kλH are nonzero, that is, where both constituents are radiating. Thus the terms in the integral represent overlap regions in the spectrum in which two or three components are radiating. The total emittance ε  is then the sum of the three individual emittances, computed as if the other constituents were absent minus a correction term for spectral overlap. For the simplified condition of gray constituents,

 

                                       (D-29)

 

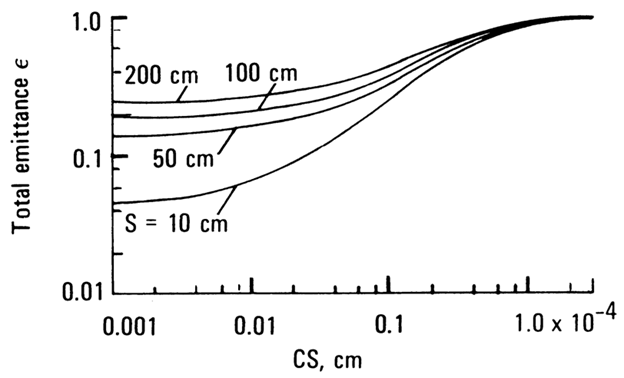
Results for the spectral-overlap terms were calculated in Felske and Tien (1973, 1975) by using the form of the CO2 and H2O vapor absorption bands and the soot absorption coefficient kλ = Ck/λ discussed earlier. Typical emittances are in Fig. D-9. For low values of CS the soot concentration is low, especially when S is high. Hence the left sides of the curves are dominated by the gas emittance, and the vertical displacement of the curves shows the increase in gas emittance with path length. As CS is increased from 0.001, the curves are somewhat horizontal (especially at high S, which corresponds to low Q as the soot concentration is not sufficient to increase ε for the mixture significantly. For larger CS the soot begins to dominate, and for all the path lengths shown, ε approaches 1 when CS is about 3 × 10−4 cm. This is consistent with the results in Fig. D-6.

A006x018
FIGURE D-9 
Total emittance of gas-soot suspension as a function of volume fraction of soot times path length. Gas temperature, 1600 K; total pressure, 1 atm; partial pressures: pH2O = 0.19 atm, pCO2 = 0.09 atm [Felske and Tien (1973)].

 

Since soot has a rather continuous emission spectrum, it is reasonable [Felske and Charamapoulos (1982)] to assume gray emission of soot in a nongray gas. This leads to a particularly simple form relating the emittance of the suspension to the individual emittances of the soot and gas. If there is no soot, Eq. (D-27) becomes

 

 

Then, from (D-27), if the soot is gray,

 

            (D-30)

 

The sum of gray gases model [see Eq. (9-54)] was used in Felske and Charamapoulos to represent the emittance for a mixture of soot, CO2, and H2O vapor,

 

 

where bj is a function of the soot volume fraction and the partial pressures of the CO2 and H2O. This model was used in Smith et al. (1987) to compute radiative transfer for a gas-soot mixture between parallel plates. Kunitomo (1974) gives results for the ratio, in a flame, of the soot-cloud emittance to the emittance of the nonluminous suspending gas; these results are for a liquid fuel. The ratio increases as the fuel carbon-hydrogen ratio is increased and as the excess air is decreased. Babikian et al. (1990) made mass absorption coefficient measurements of soot in spray combustor flames. Values were found to be between those in Dalzell and Sarofim (1969) and in Lee and Tien (1981).