THERMALRADIATION.NET

A.6 Rectangle to a Directly Opposed Parallel Rectangle

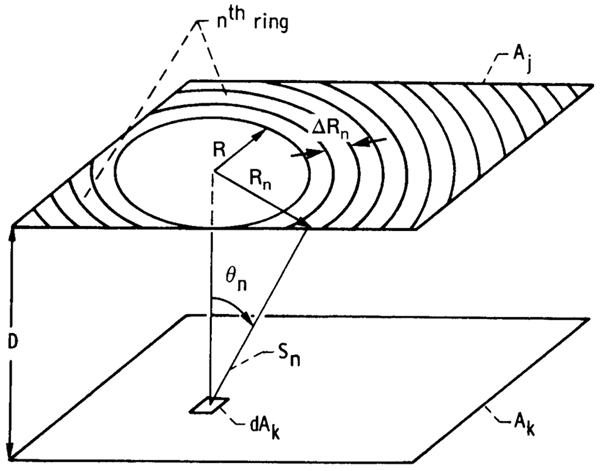
Consider, as in Fig. A-6, the exchange from a rectangle to an area element on a directly opposed parallel rectangle. The upper rectangle is divided into a circular region and a series of partial rings of small width. The contribution from the circle of radius R to  can be found from (A-6) and (A-8), for the top of a cylinder to the center of its base. For the nth partial ring, let f_n be the fraction it occupies of a full circular ring. Then, by use of (A-4), the contribution of all the partial rings to  is approximated by

FIGURE A-6 Geometry for exchange between two directly opposed parallel rectangles with intervening translucent medium.

This evaluation of  is carried out for several area patches on A_k. This is usually sufficient, so the integration over A_k can be performed as indicated by (10-62) to yield

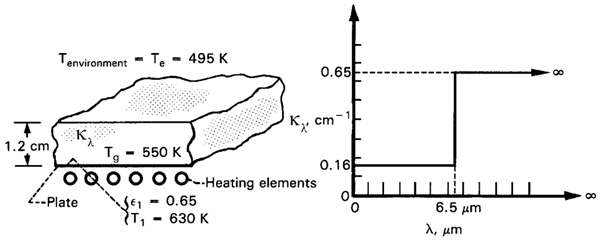
EXAMPLE A-1 A nongray, absorbing-emitting plane layer with k_λ as in Fig. A-7 is 1.2 cm thick and is on top of an opaque diffuse-gray infinite plate. The plate temperature has been raised suddenly, so the layer is still at its initial uniform temperature. What is the net heat flux being lost from the plate-layer system? Neglect heat conduction effects in the layer, and neglect any reflections at the upper boundary of the layer.

FIGURE A-7 Plane layer of nongray absorbing-emitting material.

The uniform environment above the layer acts as a black enclosure at T_e. Equation (10-77b) can be applied directly by integrating in two spectral bands and using E_λ2 = 1. The geometric-mean transmittance factors are obtained from Eq. (A-13) as   . This yields

Inserting the values F_0→6.5×630 = 0.4978, F_0→6.5×550 = 0.3985 and F_0→6.5×495 = 0.3220 yields q = 2954 W/m².