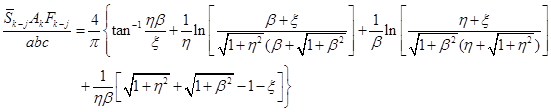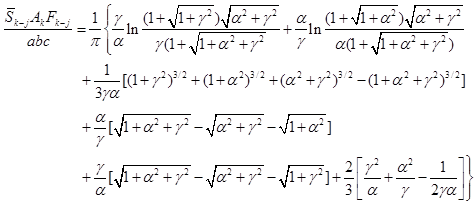THERMALRADIATION.NET

A.7 Geometric-Mean Beam Length for Spectral Band Enclosure Equations

For use in the spectral band enclosure equations (10-82), the absorption integral in (10-85) must be evaluated between pairs of enclosure surfaces for the wavelength bands involved. When more than a few bands absorb appreciably, the enclosure solution requires considerable computational effort. A simplification was developed by Dunkle (1964) by assuming that the integrated band absorption _l(S) is a linear function of path length. This has some physical basis, as it holds exactly for a band of weak nonoverlapping lines [Eq. (9-16)]. Also, it is the form of some of the effective bandwidths in Eq. (9-32). As shown in Dunkle by means of a few examples, reasonable values for the energy exchange are obtained using this approximation. Hence, let k_l in (10-87) have the linear form from (9-27) [note that the bandwidth Δλ_l = ω in (9-27)]

                                       (A-14)

where S_c and δ are the line intensity and the spacing of the individual weak spectral lines, as in Chap. 9.

Now define a mean path length  called the geometric-mean beam length, such that α_l evaluated from (A-14) by using  will equal  from the integral in (10-85). After substituting  and  into (10-85), the relation for is

                                   (A-15)

which depends only on geometry. This integral is also obtained in Eq. (A-1) when k_λS is small (optically thin limit). In Dunkle, S_k–j values are tabulated for parallel equal rectangles, for rectangles at right angles, and for a differential sphere and a rectangle. Analytical relations for rectangles are in Eqs. (A-16a,b). For directly opposed parallel equal rectangles with sides of length a and b and spaced a distance c apart,

(A-16a)

where η = a/c, β = b/c and . The F_k–j can be obtained from Factor 4 in Appendix C. For rectangles ab and bc at right angles with a common edge b,

      (A-16b)

where α = a/b and γ = c/b. The F_k–j is obtained from Factor 8 in book Appendix C. Results for equal opposed parallel rectangles are in Fig. A-8, and values for equal parallel rectangles and for rectangles at right angles are in Tables A-1 and A-2. Other  values are referenced by Hottel and Sarofim (1967) In Anderson and Hadvig (1989), values are obtained for a medium in the space between two infinitely long coaxial cylinders.

FIGURE A-8 Geometric mean beam lengths for equal parallel rectangles [Dunkle (1964)].

For a medium at uniform conditions, the geometric-mean beam length can be used in the effective-bandwidth correlations in Chap. 9 to obtain . Using Δλ_l obtained in the Next Page paragraph yields  from Eq. (12-54) and  from . Then (10-82) and (10-83) can be solved for q_l,k for each wavelength band l. The total energies at each surface k are found from a summation over all bands

                                       (A-17)

The wavelength span Δλ_l of each band is needed to carry out the solution. As discussed after (9-24), this span can increase with path length. Edwards and coworkers [Edwards and Nelson (1962), Edwards (1962), Edwards et al. (1967)] give recommended spans for CO₂ and H₂O vapor; these values, in wave number units, are in Table A-3 for the parallel-plate geometry. For other geometries, Edwards and Nelson give methods for choosing approximate spans for CO₂ and H₂O bands. Briefly, the method is to use approximate band spans based on the longest important mass path length in the geometry being studied. With this in mind, the limits of Table A-3 are probably adequate for problems involving CO₂ and H₂O vapor.