|
C. BENCHMARK
SOLUTIONS FOR VERIFICATION OF RADIATION SOLUTIONS
In this section, benchmark solutions are presented for
comparison verification of numerical codes. Besides the tables presented here,
additional benchmark solutions are in Table 11-2; Burns et al. (1995c); Hsu
and Tan (1996); Hsu and Farmer (1997); Tan et al. (2000), and
Coelho et al. (2003).
TABLE C-1 Incident
radiation
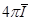 and z-component of radiative flux qz
in cube of side length 2c exposed to uniform diffuse
incident radiation qi on bottom surface z
= −c with nonhomogeneous gray extinction coefficient
b = (0.05/c) + (0.45/c)
{[1−(x2/c2)] [1−(y2/c2)][1−(z2/c2)]}2,
isotropic scattering, and scattering albedo w.
Results tabulated along line z,
x = y = 0.
Results are by numerical quadrature using 17 quadrature points (QM17) [Wu et al.
(1996)] (origin of coordinates is at cube center).
|
z/(2c)
|
|
|
|
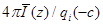
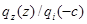
w = 1.0
|
w = 0.5
|
w=
1.0
|
w = 0.5
|
|
−0.49529
|
2.0674
|
2.0205
|
0.9466
|
0.9746
|
|
−0.47534
|
1.9955
|
1.9427
|
0.9410
|
0.9691
|
|
−0.44012
|
1.8730
|
1.8107
|
0.9246
|
0.9525
|
|
−0.39076
|
1.7066
|
1.6302
|
0.8883
|
0.9150
|
|
−0.32884
|
1.5055
|
1.4120
|
0.8251
|
0.8478
|
|
−0.25635
|
1.2837
|
1.1745
|
0.7359
|
0.7508
|
|
−0.17562
|
1.0588
|
0.9416
|
0.6311
|
0.6355
|
|
−0.08924
|
0.8487
|
0.7345
|
0.5259
|
0,5197
|
|
0.00000
|
0.6667
|
0.5657
|
0.4325
|
0.4180
|
|
0.08924
|
0.5196
|
0.4374
|
0.3566
|
0.3374
|
|
0.17562
|
0.4081
|
0.3451
|
0.2987
|
0.2778
|
|
0.25635
|
0.3280
|
0.2813
|
0.2560
|
0.2357
|
|
0.32884
|
0.2729
|
0.2384
|
0.2252
|
0.2066
|
|
0.39076
|
0.2365
|
0.2100
|
0.2033
|
0.1867
|
|
0.44012
|
0.2131
|
0.1917
|
0.1882
|
0.1733
|
|
0.47534
|
0.1989
|
0.1803
|
0.1785
|
0.1647
|
|
0.49529
|
0.1914
|
0.1744
|
0.1734
|
0.1602
|
TABLE C-2 Integrated
intensity
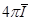and surface heat flux distributions qz,
in cylinder with diameter 2ro = height
zo
exposed to uniform collimated incident flux qi
= 1 on top surface z = 0 (positive z extends vertically
downward) with nonabsorbing gray homogeneous isotropic scattering, scattering
coefficient σs,
and optical thickness tzo
= sszo
= 0.25. Results tabulated along radius 0 < r
< ro
at z1 and
z2, and along axial position 0 < z < zo
at r1 and r2.
Results by numerical quadrature using 17 quadrature points (QM17) [Hsu et
al. (1999)]a
|
tr/tro
|
|
|
|
|
|
|
|
|
|
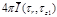
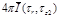
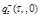
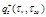
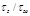
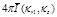
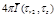
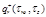
0.015625
|
1.08356
|
0.85828
|
0.04490
|
0.81969
|
0.015625
|
1.08356
|
1.04819
|
0.02810
|
|
0.078125
|
1.08344
|
0.85819
|
0.04484
|
0.81964
|
0.078125
|
1.09101
|
1.04359
|
0.03485
|
|
0.140625
|
1.08313
|
0.85790
|
0.04464
|
0.81944
|
0.140625
|
1.08377
|
1.03439
|
0.03913
|
|
0.203125
|
1.08260
|
0.85742
|
0.04434
|
0.81915
|
0.203125
|
1.07618
|
1.02194
|
0.04052
|
|
0.265625
|
1.08188
|
0.85678
|
0.04390
|
0.81873
|
0.265625
|
1.06548
|
1.00914
|
0.04168
|
|
0.328125
|
1.08096
|
0.85595
|
0.04337
|
0.81824
|
0.328125
|
1.05352
|
0.99588
|
0.04252
|
|
0.390625
|
1.07980
|
0.85490
|
0.04271
|
0.81761
|
0.390625
|
1.04008
|
0.98229
|
0.04302
|
|
0.453125
|
1.07844
|
0.85370
|
0.04194
|
0.81689
|
0.453125
|
1.02603
|
0.96805
|
0.04293
|
|
0.515625
|
1.07688
|
0.85233
|
0.04106
|
0.81609
|
0.515625
|
1.01082
|
0.95352
|
0.04252
|
|
0.578125
|
1.07509
|
0.85076
|
0.04006
|
0.81519
|
0.578125
|
0.99534
|
0.93892
|
0.04194
|
|
0.640625
|
1.07303
|
0.84899
|
0.03892
|
0.81417
|
0.640625
|
0.97851
|
0.92381
|
0.04088
|
|
0.703125
|
1.07059
|
0.84686
|
0.03749
|
0.81286
|
0.703125
|
0.96127
|
0.90835
|
0.03942
|
|
0.765625
|
1.06747
|
0.84405
|
0.03557
|
0.81106
|
0.765625
|
0.94304
|
0.89258
|
0.03771
|
|
0.828125
|
1.06363
|
0.84070
|
0.03334
|
0.80902
|
0.828125
|
0.92268
|
0.87656
|
0.03583
|
|
0.890625
|
1.05879
|
0.83654
|
0.03064
|
0.80660
|
0.890625
|
0.90140
|
0.85956
|
0.03307
|
|
0.984375
|
1.04819
|
0.82775
|
0.02527
|
0.80204
|
0.984375
|
0.85828
|
0.82775
|
0.02462
|
atr1=tro/64,
tr2=63tro/64,
tz1=tzo/64,
tz2=63tzo/64.
|