|
This relation is valid for εR,s
> 0.6. Based on these results, an estimate for εR,eff
is
In a companion paper, Xia and Strieder (1994b) provide a more
complex but more accurate relation for the upper bound on bed emissivity.
Equations (B-7) and (B-8) contain the assumption of independent scattering, so
the bed characteristics must conform to the constraints of Eqs. (B4) or (B-5).
Argento and Bouvard (1996) revisited the work of Yang et al. (1983), and
were able to use Monte Carlo results evaluated in the bed interior, thus
eliminating the problem of indeterminate bed height in random packing.
Göbel et al. (1998) have further extended Monte Carlo analysis to account
for the effect of inhomogeneities inside nonopaque spherical particles on the
radiative scattering from individual spheres. Results are compared with the
limiting cases of transparent refracting spheres, and purely reflecting solid
spheres. Independent scattering must be assumed in the approach used, and the
spheres are also assumed to be large compared with the wavelength of the
incident radiation.
Tancrez and Taine (2004) implemented a Monte Carlo technique for small
pl/D for recovering
the absorption, scattering, and phase function characteristics of a dispersion
of overlapping opaque spheres.
Fibers and fiber layers.
Glass-fiber insulations generally have very high porosities, so that even
though the fiber diameter is in the range where dependent scattering might be
important, the fiber spacing is so large that dependent effects can be
neglected. Tong et al. (1983) measured the spectral transmittance of fibrous
insulation layers using radiation from a 1300K blackbody source. A two-flux and
a linear anisotropic scattering model were used to invert the transmittance data
and find the effective radiative conductivity of the fiber layers for use in
multi-mode heat transfer calculations. White and Kumar (1990) considered
interference affects among parallel fibers.
Nicolau et al. (1994) investigated methods for experimentally determining
the spectral optical thickness, albedo, and four parameters describing a
scattering phase function. They present data for fiberglass insulation and
silica fiber-cellulose insulation.
Kudo et al. (1995) and Li et al. (1996)
analyzed transfer through a bed of randomly oriented fibers, and a bed of fibers
that are randomly oriented but lie in planes parallel to the bed surface.
Far-field scattering was assumed to occur from individual fibers. Comparison
with available experimental results for transmission through fiber beds was
quite good.
The anisotropic extinction coefficient e*(T)=b*(T)
/r of rigid fiber insulation with various anisotropic fiber orientations
was calculated for independent scattering by Marschall and Milos (1997). The
authors used basic electromagnetic theory to predict values of e*(T) and
compared the difference in radiative transfer that results from the use of the
assumption of isotropic properties in the radiative conductivity for the
diffusion equation. Differences of over 20 percent were found in a number of
cases. The results for the anisotropic case are shown to be
scalable within 5 percent of the exact calculation by superposing the results
for a matrix of anisotropic fibers and the results for fibers normal to the
incident radiation. No data for e*(T) are given.
When fibers are coated with a thin metal surface, their radiative
properties are greatly changed. Dombrovsky (1998) has provided predictions of
the scattering efficiency and extinction coefficient of fibers with various
coatings in the infrared and microwave regions of the spectrum. All results are
under the assumption of independent scattering. Other research on the properties
of woven fibers is in and Kumar and White (1995), and scattering from single
cylinders is treated in Radzevicius and Daniels (2000). Lee and Cunnington
(1998, 2000) give reviews of analytical methods, and also analyze combined
radiation/conduction.
|
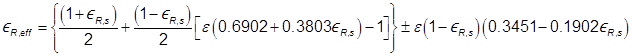 (B-8)
(B-8)