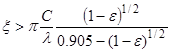|
Radiative Property Prediction
If a simple geometry is representative of a porous material,
it is possible to predict the equivalent radiative properties of a homogeneous
medium using radiative transfer analysis based on surface-surface interactions.
Cell models
Measured Properties of the Equivalent Homogeneous Material
Most measurements of radiative properties are made by
inferring the detailed properties from measurements of transmission or
reflection of radiation from the porous material. Inversion of these
measurements using methods outlined in Chap. 8 is then used to find the best set
of scattering coefficient, absorption coefficient and phase function that will
predict the measured effects.
Two problems are inherent in these measurements. First, inverse
techniques are susceptible to large uncertainties in the inferred values that
depend on the experimental uncertainty in the measured values, and there are
questions of uniqueness as well (Chap. 8). Second, the model of radiative
transfer that is used in the inversion may have particular assumptions embedded
within it. For example, a simple phase function behavior (isotropic, linearly
anisotropic, etc.) may be assumed to simplify the radiation model used in the
inversion. If this is done, then the resulting values of inferred absorption and
scattering coefficient will depend on that assumed type of phase function. It
follows that the radiative model used in describing radiation in a porous
material must use the same assumptions, or the absorbing and scattering
coefficients will not be compatible. This may be overlooked when reported
properties are taken from the literature and then using them in an incompatible
model of radiative transfer.
Dependent scattering
For spherical particles, Kaviany and Singh (1993) recommend that
independent scattering can be assumed when the criterion
is met, where C is the interparticle clearance
distance. This criterion can also be written as
where the clearance parameter xC
= pC/l. If this
criterion is not met, near-field effects must be considered. This result was
derived for porosities typical of rhombohedral packing,
e » 0.26, but
dependent scattering in packed beds remains an important effect for bed
porosities as high as 0.935, and the effect is most pronounced for opaque
particles. Both the porosity requirement and the relation between C and
l [Eqs. (B-4) or
(B-5)] must be satisfied before the assumption of independent scattering can be
used with confidence. Brewster and Tien (1982) provided the criterion for
independent scattering as
where the independent scattering region (i.e., deviation of
more than five percent from independent scattering results) is demarcated when
C/l = 0.5 is
inserted into the equation [Tien (1988)]. This relation is based on far-field
interference effects. |