THERMALRADIATION.NET

A: Derivation of Geometric Mean Beam Length Relations

The Geometric Mean Beam Lengths depend on both geometry and wavelength through the definitions

                                    (A-1)

                                                            (A-2)

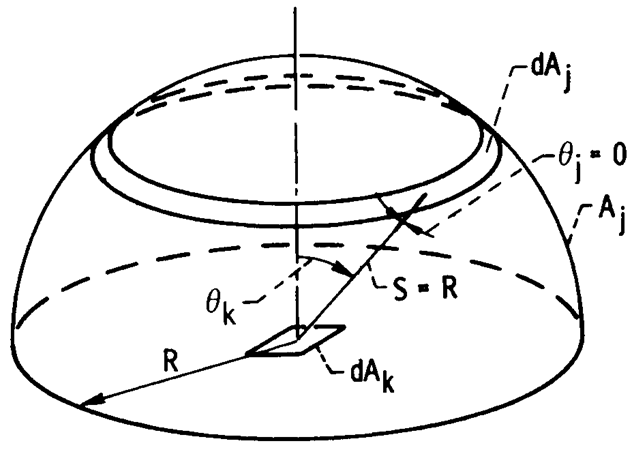
The double integral in (A-1) must be evaluated for various orientations of surfaces A_j and A_k; the result will depend on k_λ.  Derivations for some specific geometries are now considered.

A.1 Hemisphere to Differential Area at Center of its Base

Let A_j be the surface of a hemisphere of radius R, and dA_k be a differential area at the center of the base (Fig. A-1). Then (A-1) becomes, since S=R and = 0,

FIGURE A-1 Hemisphere filled with isothermal medium.

The convenient dA_j is a ring element dA_j = 2πR² sin _k d _k, and the factors involving R can be taken out of the integral. This gives

With  and , this reduces to

                                                                                          (A-3)

This especially simple relation is used later in the concept of mean beam length where radiation from an actual volume of a medium is replaced by that from an equivalent hemisphere.